regla de correspondencia

La regla de correspondencia que da lugar o establece la forma en que los elementos del primer conjunto se relacionan con el elemento (a los elementos, en caso de las relaciones), del segundo conjunto, puede representarse de diversas maneras. 

Tal como observaste en el manejo de las representaciones de las funciones. 

Explícitamente mediante el empleo de un diagrama sagital o tabla; también en la grafica y la relación matemática utilizada.

La clasificación que en principio nos resulta útil para asociar formas graficas con las analíticas, incorporando el conocimiento que tenemos acerca de ello, es agrupar las funciones según sus representaciones analíticas o ecuaciones que las define.

imagen de una función

Para entender muy bien qué es la imagen de una función, antes hay que tener muy claro qué es el dominio de una funcion.Te recuerdo que el dominio de una función es el rango de valores de x para los que existe f(x), es decir, los valores de x, para los que f(x) tiene un resultado.

Gráficamente, el dominio se mira en el eje x, ya que son los valores de x para los que la función existe, es decir, la función está representada encima.

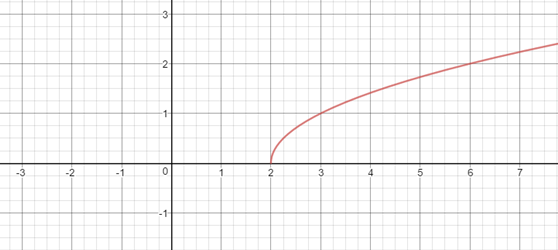
Por ejemplo, tenemos la siguiente función:

¿Cuál será su dominio?

Su dominio es el rango de valores de x para los que la función está representada encima (la función existe). Te lo marco en color azul:

Por tanto, el domino de esa función es:

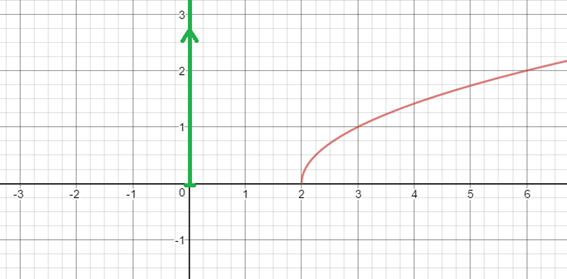
Ahora bien, ¿cuál es la imagen de esta función? Y por cierto. ¿qué es la imagen de una función?

la imagen es el rango de los valores de f(x)para los que existe un valor de x

A la imagen de una función también se le puede llamar recorrido o rango.

Dicho con otras palabras, son los valores de f(x) en los que existe la función.

Gráficamente se mira en el eje y, (ya que f(x) e y, es lo mismo). Por tanto, la imagen de la función del ejemplo anterior, son los valores que están en el eje y, para los cuales existe la función. Te lo marco en verde:

Por lo que la imagen de esa función sería:

dominio y rango

es el conjunto de números que cumplen la sustitución (tabulación) de una regla de correspondencia f(x)=y; este conjunto llamado dominio está ubicado en el eje “x” (ordenadas).

Se expresa de la siguiente forma: Domf o Df

rango de una funcion 

es el conjunto de números que dependen de la sustitución (tabulación) de los valores que puede tomar “x”, es decir, del dominio. Este conjunto de números es llamado “rango” y está ubicado en eje “y” (abcisas).

A continuación ejemplificaremos el método para obtener el dominio y el rango de la función lineal, la cual pertenece a la categoría de funciones algebraicas.

Función lineal:

Es de la forma: f(x)=ax+b

Donde: a es la pendiente y b la ordenada al origen

Su dominio es: Df= (-∞,∞)

Su rango es: Rf=(-∞,∞)

relaciones y funciones

Relación es la correspondencia de un primer conjunto, llamado Dominio , con un segundo conjunto, llamado Recorrido o Rango , de manera que a cada elemento del Dominio le corresponde uno o más elementos del Recorrido o Rango.
Por su parte, una funcion es una relación a la cual se añade la condición de que a cada valor del Dominio le corresponde uno y sólo un valor del Recorrido.

De las definiciones anteriores podemos deducir que todas las funciones son relaciones , pero no todas las relaciones son funciones.

También debemos agregar que toda ecuación es una Relación , pero no toda ecuación es una Función.

Dados dos conjuntos A y B una relación definida de A en B es un conjunto de parejas ordenadas ( par ordenado ) que hacen verdadera una proposición; dicho de otro modo, una relación es cualquier subconjunto del producto cartesiano A x B

Ejemplo 1.

Si A = {2, 3}  y B = {1, 4, 5}, encontrar tres relaciones definidas de A en B.

Solución

El producto cartesiano de A x B está conformado por las siguientes parejas o pares ordenados:

A x B = {(2, 1), (2, 4), (2, 5), (3, 1), (3, 4), (3, 5)}

INECUACIONES

Una inecuacion es una desigualdad algebraica en la cual los conjuntos (miembros) se encuentran relacionados por los signos ${\displaystyle <}$ (menor que), ${\displaystyle \leq }$ (menor o igual que), ${\displaystyle >}$ (mayor que) y ${\displaystyle \geq }$ (mayor o igual que). Por ejemplo:

${\displaystyle 2x<2}$ o ${\displaystyle 3x-2<9}$

Estas expresiones algebraicas son inecuaciones siempre y cuando las variables tomen valores que satisfagan la desigualdad.

su clasificacion es la siguiente:

Los criterios más comunes de clasificación del ejemplo: ${\displaystyle x<0}$.

• De dos incógnitas. Ejemplo: ${\displaystyle x<y}$.
• De tres incógnitas. Ejemplo: ${\displaystyle x<y+z}$.
• etc.

Según la potencia de la incógnita,

• De primer grado o lineal. Cuando el mayor exponente de la incógnita de la inecuación es uno. Ejemplo: ${\displaystyle x+1<0}$.
• De segundo grado o cuadrática. Cuando el mayor exponente de cualquiera de sus incógnitas es dos. Ejemplo: ${\displaystyle x^{2}+1<0}$.
• De tercer grado o cúbica. Cuando el mayor exponente de cualquiera de sus incógnitas es tres. Ejemplo: ${\displaystyle x^{3}+y^{2}<0}$.